Analysis of Under Reinforced Concrete Beam Section According to BS Codes

Most singly reinforced sections will be under-reinforced in practice. When the beam is under-reinforced, steel will deform before concrete. This will lead to cracks appearing on the beam bottom, indicating failure. If the beam is over reinforced, then concrete will fail before steel, and hence, the collapse will be sudden.

To be under-reinforced;

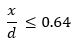
where;

x = Depth of the neutral axis

d = Effective depth of the beam

Let’s work-out a problem to see how we can analyze an under-reinforced beam section for flexure.

Determine the lever arm of the beam section given below and find out its moment of resistance.

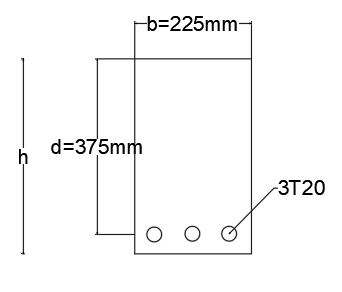
Characteristic strength of concrete = f_cu = 25 Nmm^-2

Yield strength of steel = f_y = 460 Nmm^-2

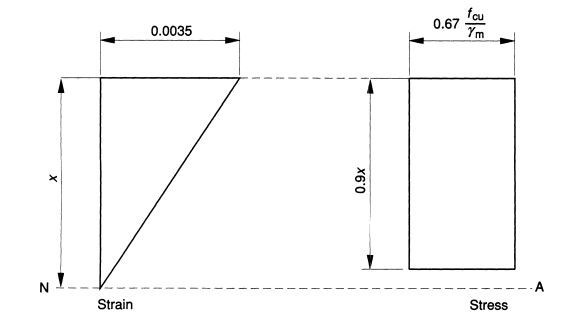
Simplified stress block for concrete at ULS (Ultimate Limit State); BS 8110-1:1997

Calculation

Area of steel = 3 r² = 3* *(10)²= 942.47 = 942.5 mm²

For under reinforcement we assume steel yields before concrete undergo maximum compression.

Assuming the steel has yielded;

T = (0.87).f_y. A_s = (0.87) (460 Nmm^-2) (942.5mm²) = 377188.5 = 377189N

Hence, by balancing tension and compression

Compressive force = 377189N

Compressive force = (0.45). f_cu.b.(0.9x)

where;

f_cu = ultimate compressive strength of concrete

b = breadth of the beam

0.9x = Height of the compressive zone

Hence;

(0.45) (25 Nmm^-2) (225mm) (0.9x) =377189N

x = 165.5=166mm

Here, we assumed that steel has yielded. i.e., why fy was taken as 460 Nmm^-2 which is the maximum tension the bars would undergo (yield strength).

Now, we need to check whether our assumption is correct.

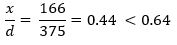
 Therefore, the beam is under reinforced. Hence, the steel has to be yielded where the original assumption is correct.

According to BS 8110-1-1997;

x = (d – z)/0.45

By subjecting z;

z = d – 0.45x, but not greater than 0.95d

where;

z = lever arm

Hence; z = d – 0.45x = 375 – (0.45) (166) = 300.3 mm = 300mm

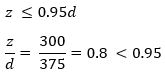
Hence; ok.

Now, let’s calculate the moment of resistance. Moment of resistance is the design moment of the beam. It is the maximum moment the beam is designed to resist. This is also called the resistance moment.

Moment of Resistance = T.z = (377189N) (300mm) = 113.16*10⁶ Nmm = 113.16 kNm