In this article, I’ll go over the fundamental theories underlying the analysis of under-reinforced concrete beam sections in accordance with EURO Codes.
Table of Contents
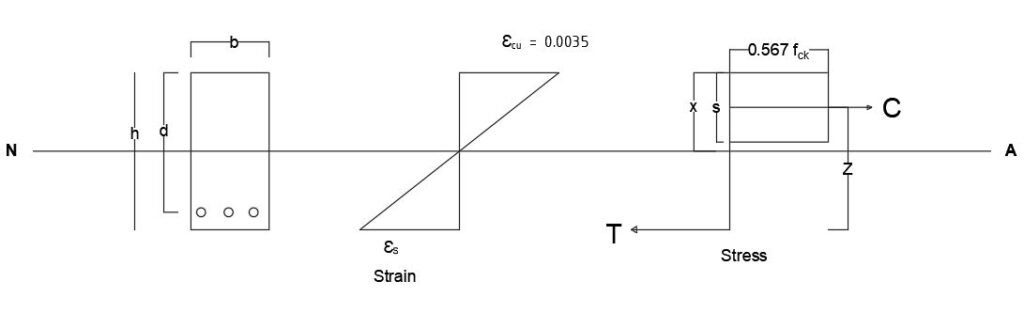
Stress and Strain distribution for Singly Reinforced Concrete Beams.
The section is called “singly reinforced” since there are reinforcing bars only in the tension zone. Steel is used to take the tension from the bottom fibers.

where;
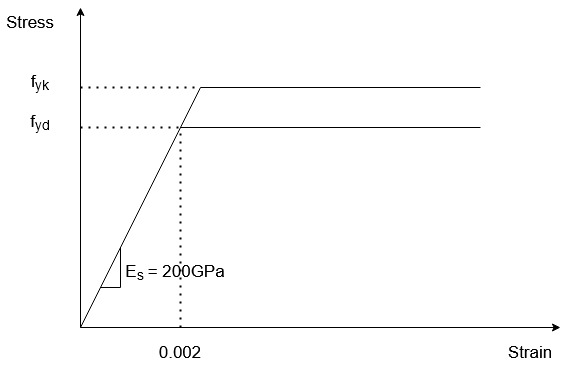
fyk= Characteristic yield strength of reinforcement
fyd = Design yield strength of reinforcement
Es = Design value of modulus of elasticity of reinforcing steel
Related equations
s=0.8x
z = d-(s/2) where; d = effective depth of the section
Stress

Strain

For singly reinforced section, the design equations can be derived as follows.
For this cross section to exist, the two forces, Fcc (compressive force of concrete) and Fst (tensile/tension force of steel), have to be equal. As a result, it provides a couple.
Hence, the resultant moment (“Mcc“)considering the compressive force on concrete (“Fcc“) can be derived as;

where;
b = breadth of the beam
s.b = area of the concrete stress block
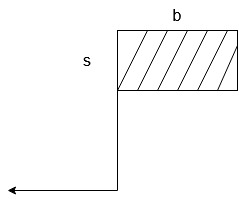
Hence,

Now, let’s find the resultant moment “M” by considering the tension force “Fst “in reinforcing steel.

According to the Eurocode and IStructE Eurocode manual, a balanced section occurs when; xbal = 0.45d.
Here, x is the distance from top fiber to the neutral axis.
This is given to ensure that failure occurs due to the yielding of steel rather than the crushing of concrete. I.e., brittle failure is avoided.
The balance sections start cracking after yielding. The over-reinforced structures will collapse suddenly without any prior warning, which is fatal.

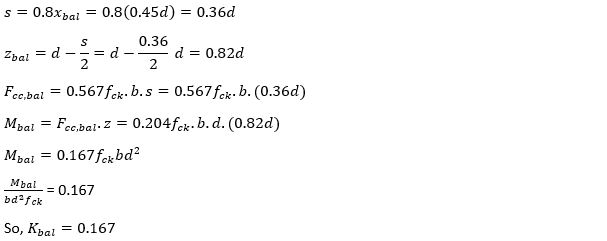
From this number, we can find whether the section is singly reinforced, balanced or not.
If K is greater than 0.167, then double reinforcement or compression reinforcement is required to bring the neutral axis depth back to 0.45d.
For economical design, K should be below 0.167.











