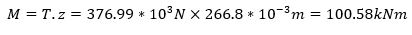Analysis of Under Reinforced Concrete Beam Section in Flexure According to Euro Codes

Determine the moment of resistance of the beam section given below.

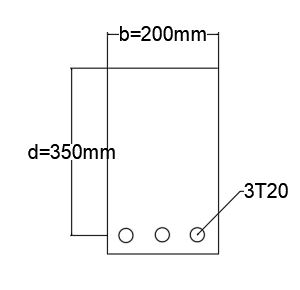
Take;

f_ck = 20MPa

f_yk = 460MPa

Calculation

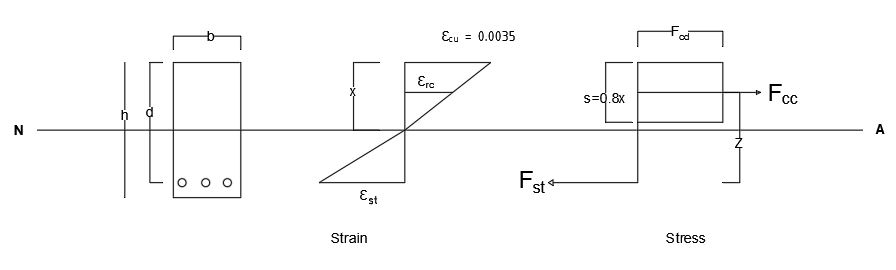
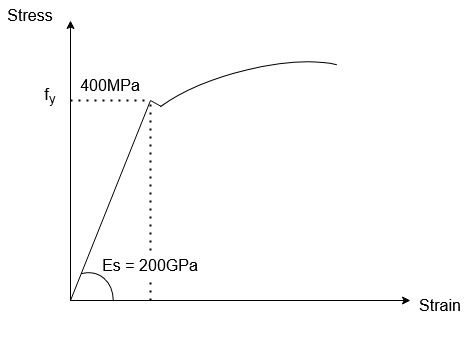
Strain

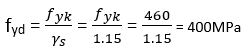
Stress

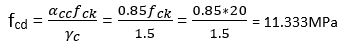
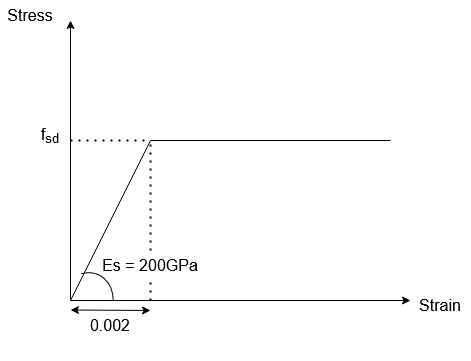
Assume the steel has yielded.

Then, the tension force in steel can be found from:

T = F_st= A_sf_yd

T=3*π(20/2)² mm² * 400Nmm^-2 = 376.99kN

Now, let’s find out the concrete compressive force C or F_cc by considering the rectangular stress distribution provided in BS EN 1992-1-1: 2004, Clause 3.1.7.3, Figure 3.5.

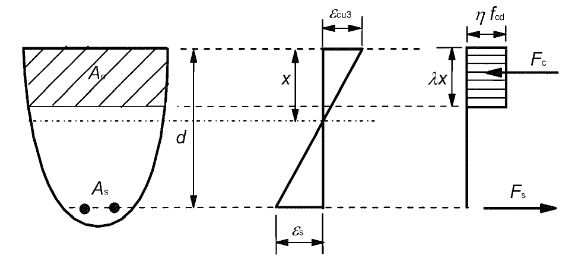
By using the rectangular stress block,

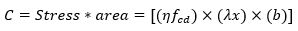
where,

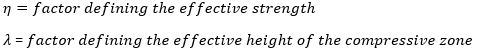
From BS EN 1992-1-1: 2004, Clause 3.1.7.3, Equation 3.19, for f_ck≤50MPa;

λ = 0.8

From BS EN 1992-1-1: 2004, Clause 3.1.7.3, Equation 3.21, for f_ck≤50MPa;

η = 1.0

Hence,

C = (0.8*11.333) * (1*x) * 200

Now let’s find the neutral axis depth (“x”) considering the balance of the section.

T = C

376.99*10³ = (0.8*11.333*) * (1*x) * (200)

x = 207.91mm

Now let’s find the actual strain in steel by considering the strain distribution provided in Fig 4.

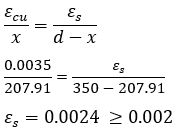
Hence, steel has yielded, and our assumption is correct.

This can also be confirmed by the BS EN 1992-1-1: 2004, Clause 3.1.7.1.

According to BS EN 1992-1-1: 2004, Clause 3.1.7.1; ε_cu=0.0035 from BS EN 1992-1-1: 2004, Table 3.1.

The condition that tensile reinforcement has yielded when the concrete strain is 0.0035 is:

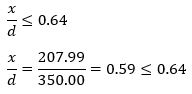
Hence, steel has yielded.

EuroCode2 recommends that (x/d) be less than 0.45; this will give enough warning before failure.

Now let’s find the lever arm (“z”).

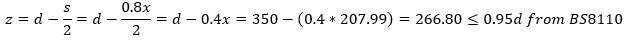
where; 0.95d =0.95*350 = 332.5mm

Hence, ok.

Now let’s find the moment of resistance (“M”).