The term 'unit weight of soil' refers to the measure of the soil’s weight per cubic meter. Typically, this is gauged in kilonewtons per cubic meter (kN/m3) within the realms of the International System of Units (SI units), or grams per cubic centimeter (g/cc) in the context of the Centimetre–Gram–Second system of units (CGS units). To clarify, the kN/m3 serves as an SI unit with global recognition, whereas g/cc is a CGS unit often employed in certain regions. These units become the cornerstone to compute various forms of soil unit weight that will be explored subsequently.
Soil density indicates how much mass of soil is packed into a specific volume. Common units include kilograms per cubic meter (kg/m3) (SI units) and grams per cubic centimeter (g/cm3) (CGS units).
This guide explains different types of unit weights of solids, formulas, and calculations with examples.
Table of Contents
Types of Unit Weight of Soil
There are 5 different types of soil unit weight that are essential for construction and civil engineering projects. Each type serves specific functions and is crucial for various calculations. Here is the summary table for five main types.
| Type of Unit Weight | Application |
| Bulk Unit Weight (γ) | Foundation design, slope stability |
| Dry Unit Weight (γd) | Soil compaction, material selection |
| Unit Weight of Solids (γs) | Soil structure analysis, quality assessment |
| Saturated Unit Weight (γsat) | Drainage studies, water retention |
| Submerged Unit Weight (γ’) | Underwater construction, hydraulic engineering |
Unit Weight of Soil Formula
The unit weight of soil is a pivotal metric in civil engineering and construction, often used to determine soil stability and strength. Various formulas allow us to calculate the different types of soil unit weights.
Key Formulas:
- Bulk Unit Weight (( $\gamma $)): $[ \gamma = \frac{W}{V} ]$ Where ( W ) is the total weight and ( V ) is the total volume.
- Dry Unit Weight (($ \gamma_d$ )): $[ \gamma_d = \frac{W_d}{V} ]$ Where ( $W_d$ ) is the dry weight of soil and ( V ) is the total volume.
- Saturated Unit Weight (($ \gamma_{\text{sat}} $)): $[ \gamma{\text{sat}} = \frac{W{\text{sat}}}{V} ]$ Where ( $W_{\text{sat}}$ ) is the saturated weight and ( V ) is the total volume.
- Submerged or Buoyant Unit Weight (($ \gamma’$ )): $[ \gamma’ = \gamma{\text{sat}} ] – \gamma{\text{water}} ]$ Where $( \gamma_{\text{water}} )$ is the unit weight of water.
- Unit Weight of Solids (( $\gamma_s$ )): $[ \gamma_s$ = $\frac{W_s}{V_s} ]$ Where ( $W_s $) is the weight of solid particles and ($ V_s$ ) is the volume occupied by them.
Step-by-Step Calculation:
- Identify the Type: Determine which unit weight type you’re calculating.
- Measure Parameters: Acquire the necessary weight and volume values.
- Apply Formula: Use the appropriate formula for calculation.
Bulk Unit Weight of Soil or Moist Unit Weight of Soil (γ)
The bulk unit weight of soil, often denoted by ($ \gamma$ ), includes both the soil particles and the moisture content. It’s a vital metric used mainly for assessing the stability of foundations and for calculating load distribution.
The formula to calculate the bulk unit weight (( $\gamma$ )) of soil is:
$[ \gamma = \frac{W}{V} ]$
Where:
($ \gamma$ ) = Bulk Unit Weight
($ W$ ) = Absolute or moist weight of soil
( $V$ ) = Volume of the soil mass
Dry Unit Weight of Soil (γd)
The dry unit weight of soil, denoted by ( $\gamma_d$ ), represents the weight of soil particles per unit volume, excluding moisture.
The formula to calculate the dry unit weight (($ \gamma_d $)) is:
$[ \gamma_d = \frac{W_d}{V} ]$
Where:
( $\gamma_d$ ) = Dry Unit Weight
($ W_d$ ) = Dry weight of the soil
($ V $) = Volume of the soil mass
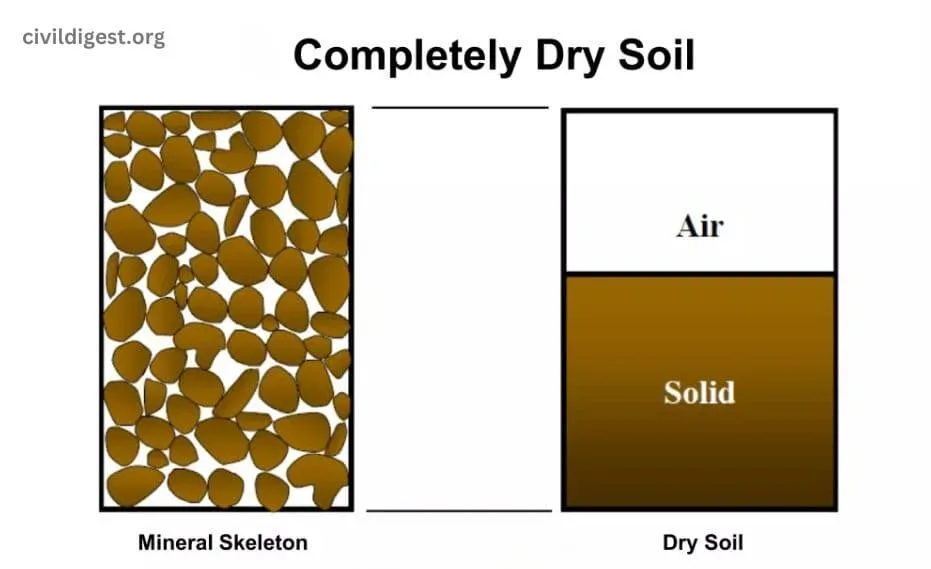
Unit weight of Solids (γs)
The unit weight of solids, often represented as ($ \gamma_s$ ), is the weight of soil particles per unit volume, disregarding voids and moisture. This value is fundamental for evaluating soil properties and structural integrity.
The formula for the unit weight of solids (( $\gamma_s$ )) is:
$[ \gamma_s = \frac{W_s}{V_s} ]$
Where:
( $\gamma_s$ ) = Unit Weight of Solids
( $W_s $) = Weight of the solid particles
( $V_s$ ) = Volume occupied by the solid particles
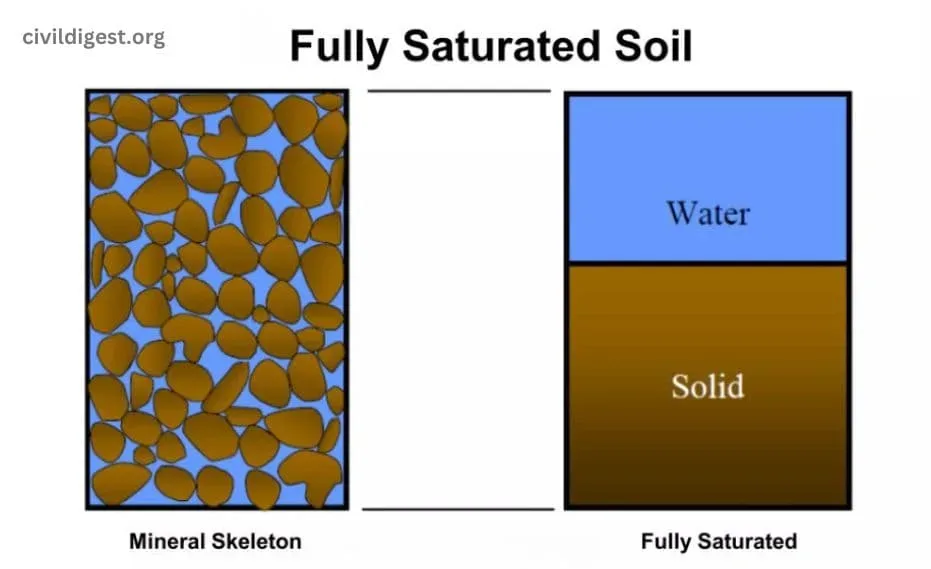
Saturated Unit Weight of Soil (γsat)
The saturated unit weight of soil, denoted by ( \gamma_{\text{sat}} ), represents the unit weight of soil when it’s fully saturated with water. It is crucial for evaluating the bearing capacity of soil and for drainage planning.
Formula:
The formula to calculate the saturated unit weight (( $\gamma_{\text{sat}} $)) is:
$[ \gamma{\text{sat}} = \frac{W{\text{sat}}}{V} ]$
Where:
( $\gamma{\text{sat}}$ ) = Saturated Unit Weight
( $W{\text{sat}}$) = Saturated weight of the soil
( $V$ ) = Volume of the soil mass
Submerged Unit Weight of Soil or Buoyant Unit Weight of Soil (γ’)
The submerged unit weight of soil, also known as buoyant unit weight, symbolized as ( $\gamma’ $), is the effective unit weight of soil when submerged underwater. It’s essential for underwater construction and slope stability analyses.
The formula to find the submerged unit weight (($ \gamma’$ )) is:
$[ \gamma’ = \gamma{\text{sat}} – \gamma{\text{water}} ]$
Where:
($ \gamma’ $) = Submerged or Buoyant Unit Weight
( $\gamma{\text{sat}}$ ) = Saturated Unit Weight
($ \gamma{\text{water}}$ ) = Unit Weight of Water
Read: Unit Weights and Densities of Soil
Convert Density of Soil to Unit Weight of Soil
In some cases, you may have the density of the soil but need its unit weight for engineering calculations. Converting between these two is straightforward.
Key Points:
- Density (($ \rho$ )): Mass per unit volume, typically in ($ \text{kg/m}^3$ ).
- Unit Weight (($ \gamma $)): Weight per unit volume, usually in ( $\text{kN/m}^3$ ).
Conversion Formula:
The formula for converting density (($ \rho $)) to unit weight (( $\gamma $)) is:
$[ \gamma = \rho \times g ]$
Where:
( $\gamma$ ) = Unit Weight
($ \rho$ ) = Density
( $g$ ) = Acceleration due to gravity (9.81 ($ \text{m/s}^2$ ))
Step-by-Step Calculation:
- Locate Density: Find the density of the soil from the given data or tests.
- Use Gravity Constant: Acceleration due to gravity is 9.81 ( $\text{m/s}^2$ ).
- Apply Formula: Multiply the density by the gravitational constant to find ($ \gamma $).
Example:
Suppose the soil density is 1800 ( $\text{kg/m}^3$ ):
$[ \gamma = 1800 \times 9.81 = 17658 \text{ N/m}^3 = 17.658 \text{ kN/m}^3 ]$
Relation Between Unit Weight and Specific Gravity of Soil
Key Concepts:
- Specific Gravity (($ G_s$ )): Ratio of the soil’s solid particle density to water density.
- Unit Weight (( $\gamma$ )): Weight per unit volume, generally in ( $\text{kN/m}^3$ ).
The Relationship:
The relation between unit weight and specific gravity is often expressed using the formula:
$[ \gamma = Gs \times \gamma{\text{water}} ]$
Where:
( $\gamma $) = Unit Weight of Soil
( $Gs$ ) = Specific Gravity of Soil
( $\gamma{\text{water}}$ ) = Unit Weight of Water $(9.81 ( \text{kN/m}^3 )$)
Step-by-Step Calculation:
- Identify Specific Gravity: Acquire the specific gravity ($ G_s$ ) from laboratory tests.
- Use Water’s Unit Weight: Standard value is 9.81 $( \text{kN/m}^3 )$.
- Apply Formula: Multiply ($ Gs$ ) by$ ( \gamma{\text{water}} )$ to find ($ \gamma$ ).
Example:
If the specific gravity ( $G_s$ ) is 2.65:
$[ \gamma = 2.65 \times 9.81 = 25.9965 \text{ kN/m}^3 ]$
Related: How many bags of topsoil in a yard
Conclusion
Understanding the various facets of soil’s unit weight is more than just a technical requirement—it’s a cornerstone for robust and safe engineering designs. From definitions and types to crucial formulas, this comprehensive guide has equipped you with the knowledge you need for precise earthwork calculations, foundation assessments, and soil stabilization tasks.
We’ve delved into the importance of terms like Bulk Unit Weight, Dry Unit Weight, and Saturated Unit Weight, illustrating their critical roles in construction and civil engineering. Further, we’ve simplified the process of converting soil density to unit weight and elucidated the integral relationship between unit weight and specific gravity.












